Problem C1.1. Inviscid Flow through a Channel with a Smooth Bump
Overview
This problem is aimed at
testing high-order methods for the computation of internal flow with a
high-order curved boundary representation. In this subsonic flow problem, the
geometry is smooth, and so is the flow. Entropy should be a constant in the
flow field. The L2 norm of the entropy error is then used as the indicator of
solution accuracy since the analytical solution is unknown.
Governing Equations
The governing equation is the
2D Euler equations with a constant ratio of specific heats of 1.4.
Flow Conditions
The inflow Mach number is 0.5
with 0 angle of attack.
Geometry
The computational domain is
bounded between x = -1.5 and x = 1.5, and between the bump and y = 0.8, as
shown in Figure 1.1. The bump is defined as
![]()
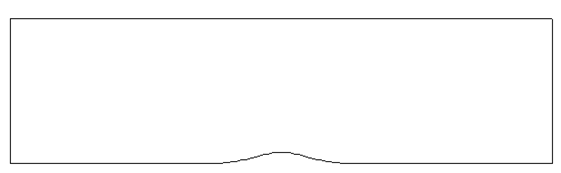
Figure
1.1 Channel with a Smooth Bump
Boundary Conditions
Left boundary: subsonic
inflow
Right boundary: subsonic exit
Top boundary: symmetry
Bottom boundary: slip wall
Requirements
1.
Start
the simulation from a uniform free stream with M = 0.5 everywhere, and monitor
the L2 norm of the density residual. Compute the work units required
to achieve a steady state. Use the following non-dimensional entropy error as
the accuracy indicator

2.
Perform
this exercise for at least three different meshes and with different orders of
accuracy to assess the performance of high-order schemes of
various accuracy.
3.
Plot the
L2 entropy error vs. work units to evaluate efficiency, and L2
entropy error vs. length scale to assess the numerical order of accuracy.
4.
Submit
two sets of data to the workshop contact for this case
a.
Error vs work units for different h and p
b.
Error vs ![]() for different h and p
for different h and p