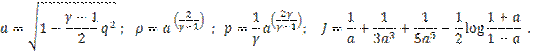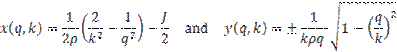Problem C1.2. Ringleb Problem
Overview
This problem tests the spatial accuracy
of high-order methods. The flow is transonic and smooth. The geometry is also smooth,
and high-order curved boundary representation appears to be critical. The exact
solution is known via ‘hodograph transformation’ [1].
Governing
Equations
The governing equations are the 2D Euler
equations with 
.
Geometry
Let k
be a streamline parameter, i.e., k = constant
on each streamline. The two stream lines for the two wall boundaries are 
for the inner wall, and 
for the outer wall. Let 
be the velocity magnitude. For each fixed 
, 
, the variable varies between 
and . For each , define the
speed of sound , density , pressure , and a quantity
denoted by 
by
|
|
|
(1) |
For each pair 
, set
|
|
|
(2) |
(a) Inflow
(b) Outflow (d) Outer wall (c) Inner wall
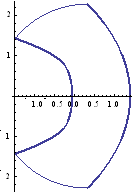
Fig. 1.2 Ringleb
geometry; thick curves: walls; thin curves: inflow and outflow boundaries.
With again , 
, and 
, the four boundaries are:
(a) inflow, 
, , and 
; (b) outflow, 
, , and ; (c) inner wall, 
and 
; and outer wall, 
and . See Fig. 1.
Exact
Solution
The exact solution is given
by (1) and (2). The flow is irrotational and
isentropic. It reaches a supersonic speed of Mach number 1.5 at location of the inner wall. The sonic line for the
problem is shown in Fig. 2. Entropy should be a constant in the flow field.
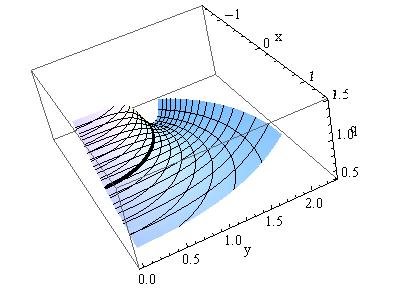
Fig. 2. Plot of velocity magnitude and streamlines for the region .
Requirements
1.
Start the simulation from the exact solution, and monitor convergence using the
L2 norm of the density residual. Compute the work units required to achieve
steady state.
2.
Similar to the smooth bump problem, use the non-dimensional 
entropy errors
as accuracy indicator. Perform the calculations for at least three different
meshes (quadruple the number of cells each time); use methods with different p to assess the performance of schemes
of various orders.
3.
To assess the efficiency of the spatial discretization,
calculate the residual (right hand side) on the densest mesh 1000 times
(equivalent to 1000 Euler forward time steps). Provides the
results in work units.
4.
Submit three sets of data to the workshop contact (above)
o
Errors vs mesh
sizes for different p
o
Errors and work units for different h (
) and p
o
Work units to complete the residual
evaluation 1000 times for various p.
References
[1] G. Chiocchia,
Exact solutions to transonic and supersonic flows. Technical
Report AR-211, AGARD, 1985.