Problem C2.1. Unsteady Viscous Flow over Tandem Airfoils

Overview

This problem is aimed to test the unsteady interaction of a vortex with a solid wall. Specifically, several cases are defined that address both unsteady pressure generation and viscous separation in a 2D framework by using a pair of airfoils. The geometry remains relatively simple and provides a test bed for several different types of analysis. In general, the time history of the lift coefficient on the aft airfoil will be used as a metric. Other quantities to assess would be the pressure distribution on the two airfoils and the total circulation in the problem obtained by integrating the vorticity throughout the domain.

Governing Equations

The governing equations for this problem are the 2D compressible Navier-Stokes equations with a constant ratio of specific heats equal to 1.4 and a Prandtl number of 0.72. Compressibility is not anticipated to be a significant player in these problems. Specific conditions will be provided with each subcase.

Flow Conditions

Two different problems are defined. In each of these cases, the Mach number () is 0.2, the angle of attack (a) is , and the Reynolds number based on the chord of one of the airfoils is 10⁴.

· Case A examines the evolution of the flow field from a prescribed initial solution that is C¹. In this condition, d is the distance to the closest wall, which is often required for turbulence models. Density and pressure are initialized to their free stream values.

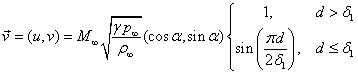
with

· Case B is closer to an impulsive start condition. Let with Density and pressure are again set to uniform free stream values.

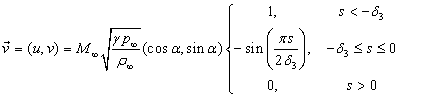
with

Geometry

The basic geometry for this case is two relatively positioned NACA0012 airfoils. As done in problem C.1.3, the airfoil geometry is given by

The leading airfoil is rotated by d about (0.25, 0) while the trailing airfoil is translated by (1 + d_sep, -d_off ). For the present case, take , d_sep = 0.5, and d_off = 0. The far field boundary can be determined such that the steady state lift coefficient of both airfoils (based on a reference length of 1 chord) varies less than 0.01 counts.

Figure 2.1 Geometry for Tandem Airfoils

Requirements

1. Perform a sensitivity study for the far field boundary condition distance required to have

the total lift and drag on both airfoils vary less than 0.01 counts.

2. Perform the indicated simulation to an elapsed time of 20 convective lengths (), maintaining a time history of the lift and drag coefficients on the aft airfoil. Perform a time step/mesh resolution study to ensure the lift coefficient is resolved to within 1 count throughout the time interval. Track the work units for this simulation. (Optional: repeat at different orders of accuracy)

3. Provide work units, the converged time history of lift and drag on the aft wing, nDOFs in the solution, and the distance to the far field boundary for each case. Submit this data to the workshop contact. Use to non-dimensionalize time.