Problem C3.4. Heaving and Pitching Airfoil in Wake
Overview
This problem is aimed at testing
the accuracy and performance of high-order flow solvers for problems with
deforming domains. An oscillating cylinder produces vortices that interact with
an airfoil performing a typical flapping motion. The time histories of the drag
coefficient on both the cylinder and on the airfoil are used as metrics, and two
test cases corresponding to different stream-wise positions of the airfoil are
studied.
Governing
Equations
The governing equations for this
problem are the 2D compressible Navier-Stokes
equations with a constant ratio of specific heats equal to 1.4 and a Prandtl number of 0.72.
Flow
Conditions
The free-stream has a mach number
(
) of 0.2 and an angle of
attack (a) of 
. The Reynolds number based
on the chord of the airfoil is 1000 (or, equivalently, 500 based on the
diameter of the cylinder).
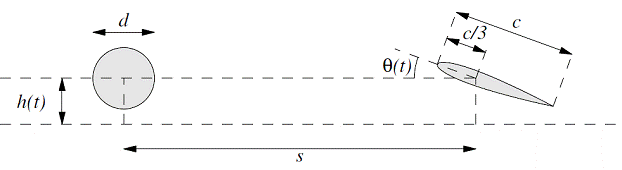
Geometry
The geometry consists of a cylinder of diameter 
centered
at the origin, and a NACA0012 airfoil with chord length 
positioned
downstream from the cylinder. The geometry is given by the modification of the 
coefficient to
give zero trailing edge thickness:
The center of the cylinder
and the 1/3 chord of the airfoil are separated by a distance 
. Both bodies are heaving in an oscillating motion 
, where 
and 
. In addition, the airfoil it pitching about its 1/3
chord by an angle 
, where the amplitude 
and the
phase shift 
.
Requirements
1. Perform the indicated simulation to an elapsed time of
100 time units (or 20 periods), for the two test cases (a) 
and (b) 
. Maintain a time history of the drag coefficients on
the cylinder and on the airfoil, and calculate the time-averaged drag
coefficients for the last (10th) period only. Perform a grid/timestep convergence study to get the time-averaged values
accurate to within 1 drag count. Record the work units.
2. Provide the work units, the converged time history of
lift and drag on the wing, nDOFs in the solution, and the distance to the far field
boundary for each case. Submit this data to the workshop contact.